布洛斯谜题

前言

布罗斯谜题，又称三神谜题。这道谜题看上去很简单，但只能用一个深不见底来形容。每当你感觉初窥门径的时候，需要思考的维度又突然多出一条，到最后只能感慨出题者和解题者强大的思维能力。由于我之前并没有过多接触谜题，即使是看着题解也难以理清思路。但愿有朝一日我能将自己的理解补充上来吧。

问

有甲、乙、丙三个精灵，其中一个只说真话，另外一个只说假话，还有一个随机地决定何时说真话，何时说假话。你可以向这三个精灵发问三条是非题，而你的任务是从他们的答案找出谁说真话，谁说假话，谁是随机答话。你每次可选择任何一个精灵问话，问的问题可以取决于上一题的答案。这个难题困难的地方是这些精灵会以「Da」或「Ja」回答，但你并不知道它们的意思，只知道其中一个字代表「对」，另外一个字代表「错」。你应该问那三条问题呢？

答

深入浅出带你看懂最烧脑逻辑题——布洛斯谜题解题思路 - 知乎 (zhihu.com)

题解

作为史上最难的逻辑题之一——布洛斯谜题，或称3神谜题（3 gods riddle）一直是大家挑战的目标，其原问题描述[1]如下：

有三位神明，分别为A，B，C。已知他们之中一位只说真话（True），一位只说假话（False），另一位随机说真话或假话（Random）。为了确定他们的身份（真神True，假神False，随机神Random），你可以向他们提问3个是非题（yes-no question），且一次只能提问其中一位。他们听得懂你的语言，但是他们只会用他们语言回答你，即“da”或者“ja”，而你不知道这两个字分别代表对或者错。

布洛斯谜题（Ted-Ed）www.bilibili.com/video/av28193104

按照Ted-Ed视频里的说法，我们的提问要够“聪明”（尽量获取最多的信息），比起问“1+1是不是等于2”，你应该问“如果我问你左边的是否是真神，你的答案会是da吗？”。这种提问一石二鸟，可以通过推断得出更多信息。因此构建提问是解谜的关键，就是问题同时包含语言及身份的信息。Ted-Ed视频中直接给出答案，并阐述了推理过程，但没有给出解题思路。若是从提问出发，虽然可以解谜，但非常容易迷失在套娃式的逻辑中，毕竟多重的推断及复杂的逻辑不是那么好理清的。网上[2,3]及维基百科上都有对这个谜题做出深入的讨论，甚至还有进阶版的。本文的目的是通过简单的组合分析，在尽量少涉及专业的背景知识及术语下给读者们讲解解题思路。

简化版谜题

两个提问确定两位神的身份
首先我们先把问题难度减低，把随机神（Random）去掉，只剩下真神（True）和假神（False）然后我们只能问2个问题，而我们还是听不懂他们的语言，那你要如何确定两位神（A，B）中哪个是真神，哪个是假神。我们可以从组合的角度出发，在简化版的谜题中，我们有4种情况（可能性）：1）da=对，A是真神、2）da=对，A是假神、3）ja=对，A是真神、4）ja=对，A是假神。而神回答的只能是da或者ja，虽然我们不懂他们的语言，但是通过两次提问的回答我们可以得到4组可能的结果：1）da da、2）da ja、3）ja ja、4）ja da。如果我们把得到的回答对应到不同情况。那么就可以得知哪位是真神，哪个词代表的是“对”。具体观察以下配对表：

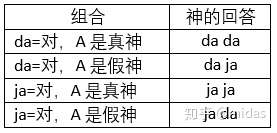
接下来我们才开始构建我们的提问（题目没有限制每位神只能回答一个提问，但是这并不影响我们的讨论，假设我们先问A再问B）。首先第一个问题要求两位神的回答一致，对于真神，这个不难。而假神的话，在不说谎的情况下他的回答必须和真神相反，然后因为说谎，他的回答才能和真神一致（负负得正）。显然直接问“1+1是否等于2？”是不行的。那要如何才能让两位神的真实相反呢？最直接的方法是问“你是真神吗”，真神的回答肯定“对”，而假神因为要说谎，所以也会回答“对”。而根据得到的回答是da还是ja，那我们就可以知道哪个代表“对”。因为已经听懂他们的语言了，那第二题就可以直接对B提问“1+1是不等于2是吗？”。

一个提问确定两位神的身份
细心的读者可能发现，如果我们不在乎da或者ja代表的“对”，而只关心神的身份，是否能靠一个提问就能得知神的身份？答案是肯定的。首先还是把我们的配对表列出：

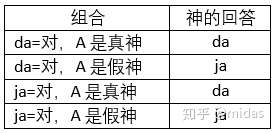
我们的提问要求不管在da或者ja代表“对”的情况下，真神只回答da，而假神只回答ja。方法和前面一样（负负得正）。之前是为了让真假神都给出一致的答案，所以提问涉及了神的身份。而这次为了在不同情况（da=对或者ja=对）下得到一致的答案，那问题就必须涉及到da和ja。比如可以提问“da代表对吗？”在da=对的情况，真神会回答da（对），而假神会回答ja（错）。在ja=对的情况，真神会回答da（错），而假神会回答ja（对）。就这样，我们可以在不了解他们语言的情况下，仅靠一个问题得知他们的身份。

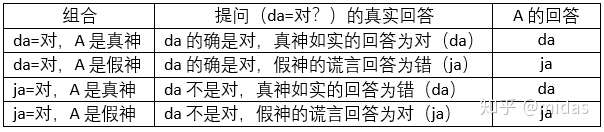
从信息学的角度，如果要知道神的身份（即A是真神或假神），我们需要1比特（2种情况）的信息。如果还要了解其语言（da=对或者ja=对），那我们需要2比特（2x2=4种情况）的信息。而神的每次回答也只能提供1比特的信息。因此根据我们所需要的信息，可以知道我们最少可以通过几个提问得到我们想要的答案。

布洛斯谜题解题思路

谜题组合分析
回到原问题，这时多了一个随机神，但是多了两个提问。从信息学的角度，三位神的身份共有3!=6种组合。如果只有2个提问，我们只能区分4种情况，因此需要三个问题（2x2x2=8）才能做出区分。

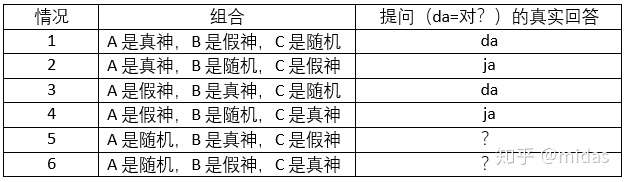
按照前面的方法构建提问，那我们会发现谜题的难点在于随机神，因为他给出回答无法提供我们任何有用的信息，因此我们要避免问到随机神。避开或者排除随机神是我们的首要目标。假设我们第一个提问的是A，前面4种情况是可以完全避开随机神，而运气不好的话遇到后两种情况（第一个就问到随机神），随机神的回答可以是da或者ja，会出现4种情况，加起来一共8种。因此原则上我们的3个提问是可以准确的解答这道谜题。

忽略神的语言 - 在理解神的语言情况下的解题思路
为了不让各位读者在复杂的逻辑种迷失，先假定我们听得懂神的语言（他们直接回答对或错）。基于前面的例子我们可以肯定，只要我们涉及的提问加入关于da和ja，那神的回答无论在da或者ja是” 对”的情况下都一致。且为了方便起见，我们把” 对”表示为1，“错”为0。由于不知道3位神的身份，我们先把他们命名为A，B和C。

前面4种情况，我们可以完全避开随机神。方法在于，我们根据他们的回答来决定接下来是问哪个。现架设A——B——C三位神坐成一排（A在左，C在右）。若他们回答是1，我们就向右边那个发出提问，0的话就向左边。如果左/右已经没神了，那就问另一端的。比如A给的回答是1就问B，A给的回答是0就向C提问（同样C给的回答是1就问A，C给的回答是0就向B提问）。有了这个规定，我们可以发现前面两道提问给出的组合分别是：

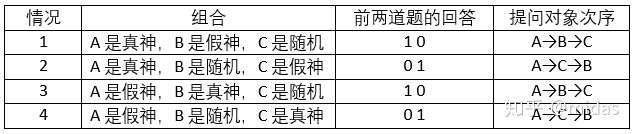
这4种情况占用了前两道回答4种组合（00，01，10，11）种的2种（01和10），而我们还有最后一个提问，因为已经避开了随机神，所以最后一个提问肯定可以得到我们所要的信息。对于情况5和6，由于A的回答可以是0或者1，那我们设计的提问就必须让第二个回答和第一个一样，这才能把A是随机神的情况区分出来，具体分析看下表：

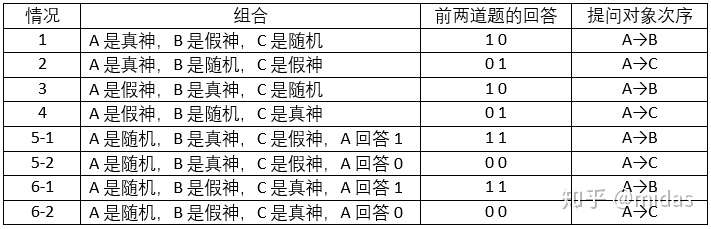
根据前面两道题的回答，我们基本可以锁定随机神的身份。11或者00说明A是随机神，01说明B是随机神，而10则说明C是随机神。排除了随机神后，我们的谜题就可以简化得上一节（只有真神和假神）一样。通过第三道提问可以直接区分真神及假神得身份，解法这里就不加赘述。接下来就是要对刚提出的方案制定前两道问题。

上一节的例子比较简单，所以直接忽略了提问的推导出过程。首先我们已知的是神的回答及神的身份，在排除神的身份（真神说真话，假神说谎）下，我们可以我们的提问的真实答案。根据这个答案，我们才能设计我们的提问。

对于第一个提问，因为情况5和6里A的回答没有意义，我们只需关注情况1到4。我们的提问在情况1和3 得到的回答必须是“对”（1），情况2和4得到的是“错”（0）。由于情况3和4的A是假神，会说反话。那么我们的提问的真实答案，在情况1和4下必须是“对”的，而2和3的情况下是“错”的。为了更好理清其中的逻辑，可以观察下表。

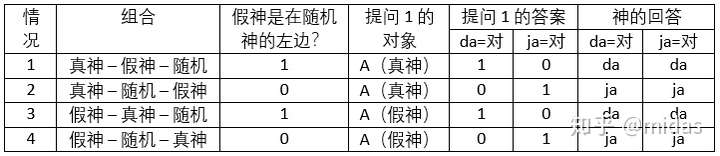
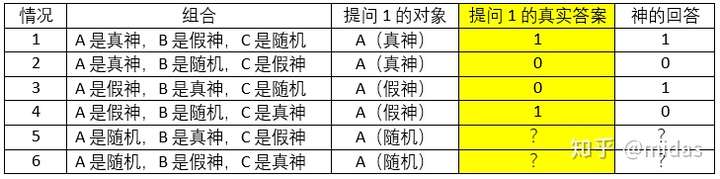通过神的回答及神的身份来推导出我们提问的真实答案（黄色）。以情况4为例，基于负负得正的原理，假神（负）和回答为0（负），我们提问得真实答案必须是“对”（1）。可以观察出在情况1和4，假神都是再随机神的左边，因此，提问1可以设为：“假神是在随机神的左边吗？”

根据上述条件，接下来如果靠观察及试错来设计我们的提问并不是很难的事。如果学过相关数理逻辑的可以对每个情况画个真值表（Truth table），然后根据真值表设计提问。这里直接给出一个比较简单的例子：“假神是在随机神的左边（按照我们的坐标系）吗？“

第一个提问解决后，那么接下来第二个提问也是用同样方法解决。具体步骤就是结合神的回答+神的身份推导出提问2的真实结果，。必须注意的是，第二道提问的对象是根据第一道提问（A）的回答来决定的。如果A回答“对”，我们就向右边那个（B）问，反之则向左边C（因为A在最左边，所以向另一端的C提问）。

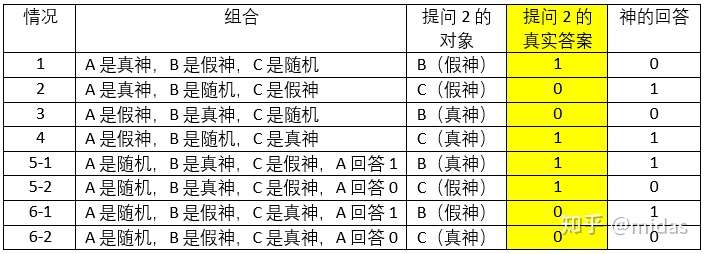
这回因为多了4种情况（一共8种）必须满足条件，因此大很多。像第一道提问那样通过几轮的试错（对他们相对位置的进行提问，如：谁在谁的左/右边），可以发现没有一个描述（神的相对位置）是可以同时满足8种情况的答案。因此我们需要结合多个描述（命题）来做出提问。

这里简单介绍逻辑学里的命题。命题的要求是可以被证实或者证伪。比如我们的第一个提问：“假神是在随机神的左边。”在情况1和4中是对（证实）的，而2和3中是错的（证伪）。另一个需要了解的概念是“与”及“或”。举个例子：“昨天下雨”和“前天下雨”这两个命题。用“与”及“或”结合的话可以得到“昨天或前天下雨”（或命题）和“昨天与前天下雨”（与命题）这两个命题。由于下雨这件事是可以证实的（不考虑时间段，假设雨下一整天），那么对于这两个或命题及与命题的判断（“对”或“错”）的，和我们直观理解的并无任何差异，具体可以参考下表：

简单做个总结，对于两个命题，如果用“或”来结合，只要其中一个命题是“对”，那或命题的结果就是“对”。而用“与”来结合，只要其中一个命题是“错”，那与命题的结果就是“错”。把上面的表抽象化，分别用M，N代表两个命题，我们可以得到以下的表（又称真值表）：

回到我们的谜题。前面发现我们的提问无法通过一个描述（神的相对位置）来满足8种情况。那我们先把现有的描述列出（这里只举其中的几种）：

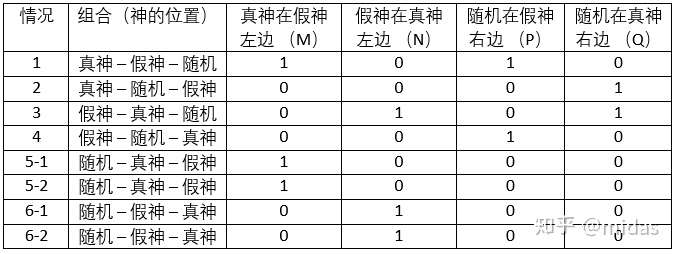
把其中两个命题用“或”或者“与”结合，在几次试错后，我们可以发现用“或”把命题M（真神在假神左边）及P（随机在假神右边）结合可以得到我们期待的结果（下表）。完成了前两个问题，我们基本可以确定随机神的身份。第3道提问只要重复简化谜题的方法就完成了。

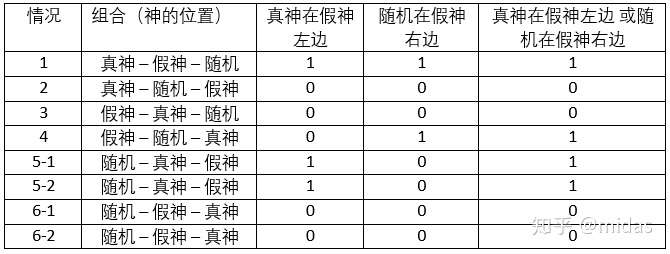
考虑不理解神的语言的情况
到目前位置，我们的解谜是在听得懂三位神的语言情况下推出来的。在听不懂他们的语言情况下，可能出现的情况还会多出一倍，即da=对或ja=对的情况。由于听懂他们的语言不是我们的目的，我们还是可以把刚才两道问题，按照简化谜题里的方式（da=对？）做修改。我们的目的是无论da=对或者ja=对，神的回答都一致（一样的表）。这两道题在两种情况下得到的结果刚好相反，要得到相同的结果，必须把ja或者da的逻辑加进去。对于提问1（假神是在随机神的左边吗？），可以修改为：“假神是在随机神的左边的答案是da吗？”

同样，我们可以规定，对于第一个提问的回答为da，我们接下来向B提问，否则向C。对于第2个提问（真神在假神左边或随机在假神右边吗？），我们同样修改为：“真神在假神左边或随机在假神右边的答案是da吗？“

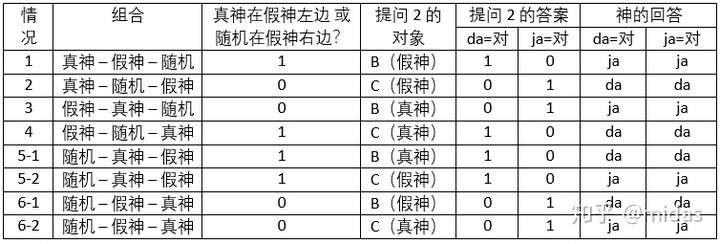
完整的答案
到目前为止，我们基本上算是完整地推导出了判断3位神的身份地方法。基于过程太冗长复杂，这里直接给个总结：

假设：
1）三位神站/坐成一排，左到右为A——B——C

策略：
1）先向A提问，A地回答为ja的话接下来对B提问，否则向C提问。
2）第3个提问和第2个都是同一位神。
3）根据提问的得到的回答可以达到8种组合，按照下表可以唯一地确定ABC三位神地身份。

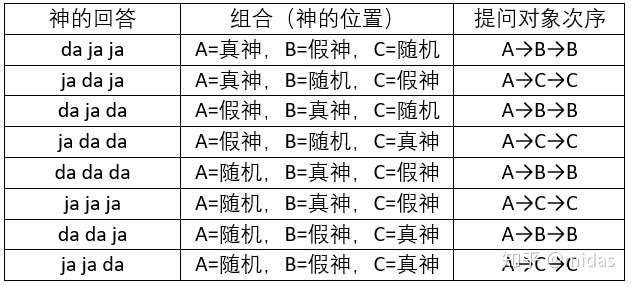
提问：
1）假神是在随机神左边的答案是da吗？
2）真神在假神左边或者随机在假神右边的答案是da吗？
3）da=对？

总结

布洛斯谜题的难点在于构建我们的提问。谜题的解法不是唯一，这里只提供一种方案。本篇主要目的是提供解题框架及思路。主要的方式是先列出所有的情况组合（神的身份，语言），然后根据神的三个回答的组合（da da ja，ja da ja，…）做出相应的配对。最后根据神的回答来定制我们的提问。此谜题的困难点在于随机神的存在，因此在做组合配对时需要加入选择策略（下一个提问的对象），来避开（或找出）随机神。由于理解神的语言并不是我们目的，我们可以先把问题简化，让我们理解神的语言，求出结果后，再把语言考虑进去。

换个说法，这种解法相当于把复杂的逻辑层层剥开，一步一步简化我们的问题设计。若一开始直接设计问题，除了毫无头绪，也很容易被复杂的逻辑搞乱而出错。当问题简化后，我们可以靠简单的试错方式设计我们的提问，即使没学过数理逻辑，也可以在有限时间内得到结果。

如果有尝试解过布洛斯谜题，就会发现假神即使是说谎，他还是提供有用的信息。最棘手的是随机神，因为我们无法判断他说的是一切真是假。这验证了一句话：最危险的从来不是谎言，而是和真相参杂在一起的谎言。从人与人之间的交往到国与国之间的博弈，处处都充斥这这个道理。变数太大的事情很少人愿意干，而喜怒无常的人让人远离。古今中外上被称为战神的人物，韩信、白起、成吉思汗、汉尼拔、凯撒等，都是靠着灵活且令人捉摸不透的方式领兵作战，在史书上封神。